Packet Switching Networks part2

ROUTING TABLES

Routing Table for Virtual circuit networks

• virtual circuit identifier determines the destination

Routing table for datagram networks

Specialized Routing

Flooding

· Principle of flooding: a node (or a packet switch) forwards an incoming packet to all ports except to the one it arrived on.

· Each node (a switch) performs the flooding process such that the packet will reach the destination as long as at least one path exists between the source and the destination.

· Flooding is a useful

o when the information in the routing tables is not available, such as during system startup,

o when survivability is required, such as in military networks.

o when the source needs to send a packet to all hosts connected to the network (i.e., broadcast delivery).

• Flooding generates vast numbers of duplicate packets

In figure, initially one packet arriving at node 1 triggers three packets to nodes 2, 3, and 4. In the second phase nodes 2, 3, and 4 send two, two, and three packets respectively. These packets arrive at nodes 2 through 6. In the third phase 15 more packets are generated giving a total of 25 packets after three phases.

The flooding needs to be controlled so that packets are not generated excessively.

How to control this?

There are three methods to reduce the resource consumption in the network

1) Use a time-to-live (TTL) field in each packet.

· When the source sends a packet, the time-to-live field is initially set to some small number.

· Each node decrements the field by one before flooding the packet. If the value reaches zero, the switch discards the packet.

· To avoid unnecessary waste of bandwidth, the time-to-live should ideally be set to the minimum hop number between two furthest nodes (called the diameter of the network).

2) Add an identifier before flooding

· Every node adds an identifier before flooding

· When a node identifies a packet that contains the identifier of the switch, it discards the packet.

· This method effectively prevents a packet from going around a loop.

3) Have a unique sequence number

• Each packet from the given source is uniquely identified with a sequence number

• When a node receives a packet, it records the source address and the sequence number

• If node discovers that packet has already visited the node, it will discard the packet

Deflection Routing

• Deflection routing was first called as Hot-potato routing.

• It requires the network to provide multiple paths for each source-destination pair.

• Each switch first tries to forward a packet to the preferred port. If the preferred port is busy or congested, the packet is deflected to another port.

• Deflection routing works well in a regular topology.

Example :- Manhattan Street network:

• Each column represents an avenue, and each row represents a Street.

• Each switch is labeled (i,j) where i denotes the row number and j denotes the column number.

• The links have directions that alternate for each column or row.

• If switch (0,2) would like to send a packet to switch (1,0), the packet could go two left and one down. However, if the left port of switch (0,1) is busy (see Figure ), the packet will be deflected to switch (3,1). Then it can go through switches (2,1), (1,1), (1,2), (1,3) and eventually reach the destination switch (1,0).

• One advantage of deflection routing is that the switch can be bufferless, since packets do not have to wait for a specific port to become available. Since packets can take alternative paths, deflection routing cannot guarantee in-sequence delivery of packets.

• Deflection routing is used to implement many high-speed packet switches where the topology is very regular and high-speed buffers are relatively expensive compared to deflection routing logic.

Shortest Path Routing

Shortest path algorithms are used to determine the shortest path based on following metrics.

The shortest path routing are Bellman-Ford algorithm and Dijkstra’s algorithm

· Possible metrics

· Hop count

· Reliability:

· Delay: sum of delays along path

· Bandwidth: “available capacity” in a path

· Load: Link & router utilization along path

· Cost: $$$

Bellman-Ford Algorithm or Ford-Fulkerson algorithm

Principle: - If each neighbor of node A knows the shortest path to node Z, then node A can determine its shortest path to node Z by calculating the cost/distance to node Z through each of its neighbors and picking the minimum.

Bellman-Ford algorithm

· Consider computations foronedestination d

· Initialization

· Each node table has 1 row for destination d

· Distance of node d to itself is zero: Dd=0

· Distance of other node j to d is infinite: Dj=µ, for j¹ d

· Next hop node nj = -1 to indicate not yet defined for j ¹ d

· Send Step

· Send new distance vector to immediate neighbors across local link

· Receive Step

· At node j, find the next hop that gives the minimum distance to d,

· Minj { Cij + Dj }

· Replace old (nj, Dj(d)) by new (nj*, Dj*(d)) if new next node or distance

· Go to send step

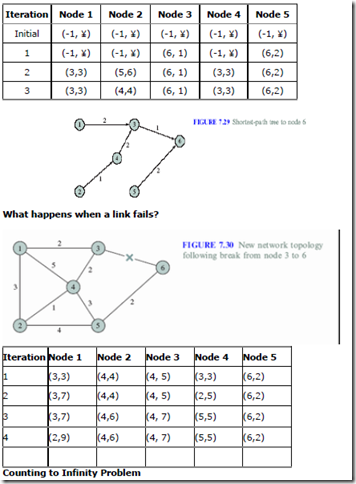
For the above figure Apply Bellman-ford algorithm to find both minimum cost from each node to the destination node 6 and the next node along the shortest path.

Each node I maintains an entry (n,Di), where n is the next node along the current shortest path and Di is the current minimum cost from node i to destination.

Initially all nodes, other than the destination node 6, are at infinite cost (distance) to node 6. Node 6 informs its neighbors it is distance 0 from itself.

Iteration 1:- Node 3 finds that it is connected to node 6 with cost of 1. Node 5 finds it is connected to node 6 at a cost of 2. nodes 3 and 5 update their entries and inform their neighbors.

Iteration 2:- Node1 finds it can reach node 6, via node 3 with cost 3. Node 2 finds it can reach node 6, via node 5 with cost 6. Node 4 finds it has paths via nodes 3and 5,

with costs 3 and 7 respectively. Node 4 selects the path via node 3. Nodes 1, 2, and 4 update their entries and inform their neighbors.

Iteration 3:- Node 2 finds that it can reach node 6 via node 4 with distance 4. Node 2 changes its entry to (4,4) and informs its neighbors.

Iteration 4:- nodes 1,4, and 5 process the new entry from node 2 but do not find any new shortest paths. The algorithm has converged.

Problem: Bad News Travels Slowly

Remedies

· Split Horizon

· Do not report route to a destination to the neighbor from which route was learned

· Poisoned Reverse

· Report route to a destination to the neighbor from which route was learned, but with infinite distance

· Breaks erroneous direct loops immediately

· Does not work on some indirect loops

Split Horizon with Poison Reverse

Source Routing

· In source routing, path to the destination is determined by the source.

· Source routing works in either datagram or virtual-circuit packet switching.

· Before sending packet, the source has to know the path to the destination in order to include the path information in the packet header.

· The path information contains the sequence of nodes to traverse and should give sufficient information to intermediate node to forward the packet.

· The below fig. shows how source routing works in datagram network.

· Intermediate switch reads header and removes the address identifying the node and forwards the packets to next node.

· Source host selects path that is to be followed by a packet

· Strict: Here, the source specifies the address of each node along the path to the destination.

· Loose: When source knows partial information of network topology, the source can use loose source routing.

Packet Switching Networks-1

1. What are the different network services provided by network layer of the packet switching networks? (Aug 06, 10M)

2. Why is packet switching more suitable than message switching for interactive applications? Compare the delays in datagram packet switching and message switching. (Jan 10, 6M) (Dec 12 10 M)

3. Compare the Bellman –Ford algorithm and Dijkstra’s algorithm for finding the shortest paths from a source node to all other nodes in a network.

(Jan 10, 6M)

4. Differentiate between virtual circuits and datagram subnets.

(July 09, 10M)(AUG 02,Feb 06 6M) (July 07, 5M)

5. Define routing and forwarding. What are the goals of routing algorithm?

(AUG 05, 6M)

6. Using Dijkstra’s algorithm find the shortest path between A and D

7. Explain hierarchical routing. (Feb 05, 6M) (July 07, 5M)

8. What are the drawbacks of flooding? (Aug 06, 4M) Define routing. Explain Bellman-Ford routing algorithm with necessary illustration. What are the drawbacks of this algorithm?

(Aug 06, 10M) (June 12 10 M)

9. Good news spreads fast; bad news propagates slowly in bellman ford algorithm.

Explain with an example. (July 07, 5M)

10. Explain Count to infinity problem. (July 06, 6M)

11. Consider the network in fig

(i) Use the Dijkstra’s algorithm to find the set of shortest path from node 4 to other node.

(ii) Find the set of associated routing table entries

(iii) find the shortest path from node 5 to other destination node and Find the shortest path tree from 5 to other nodes. (Dec 12 10 M)

12. Suppose that 64kbps PCM coded speech is packetized into a constant bit rate ATM cell stream.

i) What is the interval between production of full cells ?

ii) How long does it take to transmit the cell at 155Mbps?

iii) How many cells could be transmitted in this system between consecutive voice cells? (Jan 10 , 6M)

13. Differentiate between virtual circuit and datagram’s. Explain routing table for both.

(Dec 10, 10 M)

14D. ifferentiate between connectionless packet switching and virtual packet switching. (June/July 11 8 M)

15.Explain briefly the structure of a generic packet switch, with the help of the diagram (June/July 11 7 M)

16. With examples, Differentiate between datagram, virtual circuits and packet switching. (June 12 6 M)

17. Write a short note on ATM networks (June 12 4 M)

18. Explain Dijikstras algorithm. Solve the following problem (Dec 10 10 M)